One sample Z-tests • distributions3

Problem setup

Let’s suppose that a student is interesting in estimating how many memes their professors know and love. So they go to class, and every time a professor uses a new meme, they write it down. After a year of classes, the student has recorded the following meme counts, where each count corresponds to a single class they took:

$3, 7, 11, 0, 7, 0, 4, 5, 6, 2$

The student talks to some other students who’ve done similar studies and determines that $\sigma = 2$ is a reasonable value for the standard deviation of this distribution.

Assumption checking

Before we can do a Z-test, we need to make check if we can reasonably treat the mean of this sample as normally distributed. This happens is the case of either of following hold:

The data comes from a normal distribution.
We have lots of data. How much? Many textbooks use 30 data points as a rule of thumb.

Since we have a small sample, we should check if the data comes from a normal distribution using a normal quantile-quantile plot.

# read in the data
x <- c(3, 7, 11, 0, 7, 0, 4, 5, 6, 2)

# make the qqplot
qqnorm(x)
qqline(x)

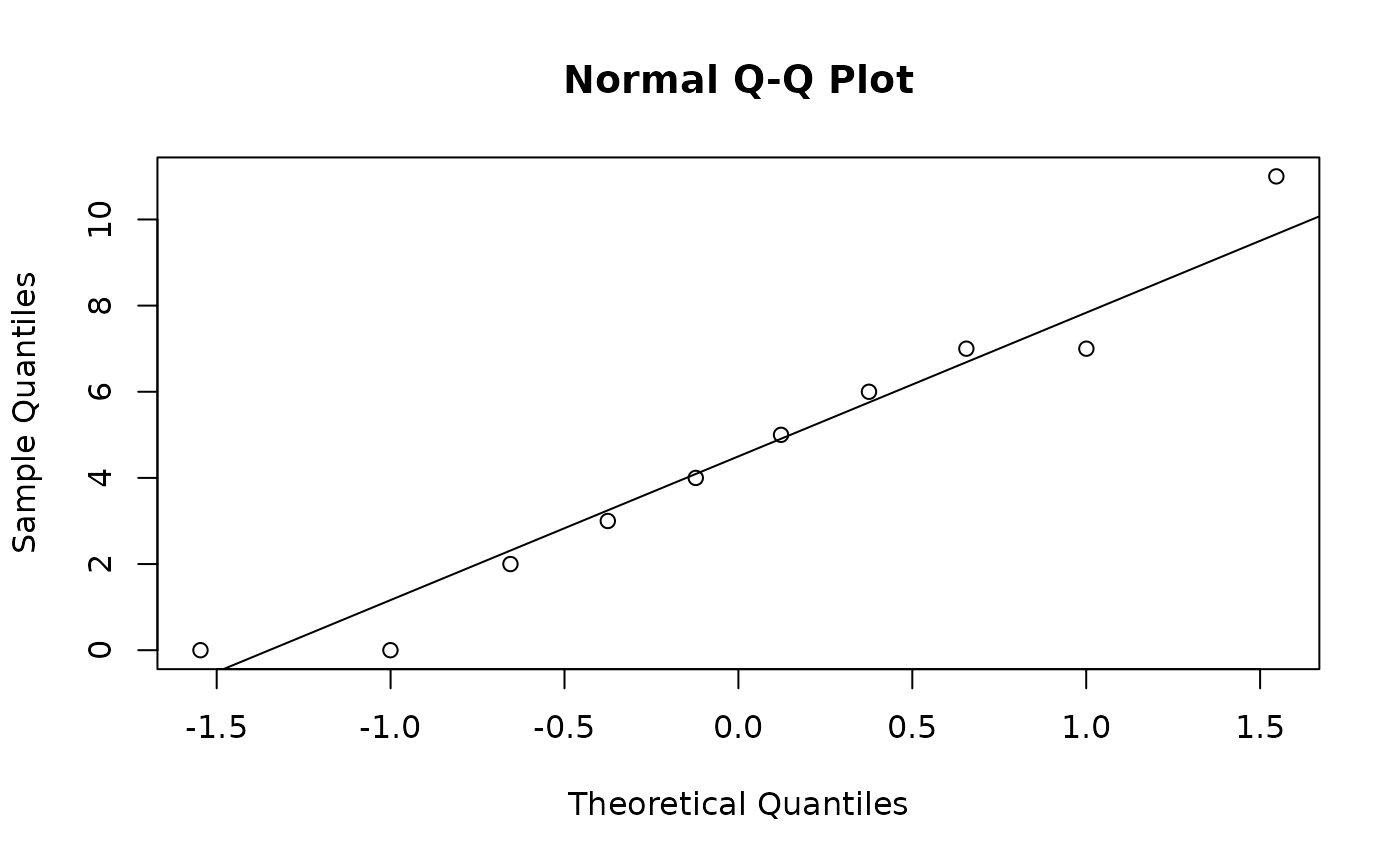
Since the data lies close the line $y = x$ , and has no notable systematic deviations from line, it’s safe to treat the sample as coming from a normal distribution. We can proceed with our hypothesis test.

Null hypothesis and test statistic

Let’s test the null hypothesis that, on average, professors know 3 memes. That is

$H_0: \mu = 3 \qquad H_A: \mu \neq 3$

First we need to calculate our Z-statistic. Let’s do this with R. Remember that the Z-statistic is defined as

$Z = \frac{\bar x - \mu_0}{\sigma / \sqrt{n}} \sim \mathrm{Normal}(0, 1)$

Calculating p-values

In R this looks like:

n <- length(x)

# calculate the z-statistic
z_stat <- (mean(x) - 3) / (2 / sqrt(n))
z_stat
#> [1] 2.371708

To calculate a two-sided p-value, we need to find

$\begin{align} P(|Z| \ge |2.37|) &= P(Z \ge 2.37) + P(Z \le -2.37) \\ &= 1 - P(Z \le 2.37) + P(Z \le -2.37) \\ &= 1 - \Phi(2.37) + \Phi(-2.37) \end{align}$

To do this we need to c.d.f. of a standard normal

library(distributions3)

Z <- Normal(0, 1)  # make a standard normal r.v.
1 - cdf(Z, 2.37) + cdf(Z, -2.37)
#> [1] 0.01778809

Note that we saved z_stat above so we could have also done

1 - cdf(Z, abs(z_stat)) + cdf(Z, -abs(z_stat))
#> [1] 0.01770607

which is slightly more accurate since there is no rounding error.

So our p-value is about 0.0177. You should verify this with a Z-table. Note that you should get the same value from cdf(Z, 2.37) and looking up 2.37 on a Z-table.

You may also have seen a different formula for the p-value of a two-sided Z-test, which makes use of the fact that the normal distribution is symmetric:

$\begin{align} P(|Z| \ge |2.37|) &= 2 \cdot P(Z \le -|2.37|) \\ &= 2 \cdot \Phi(-2.37) \end{align}$

Using this formula we get the same result:

2 * cdf(Z, -2.37)
#> [1] 0.01778809

Finally, sometimes we are interest in one sided Z-tests. For the test

$\begin{align} H_0: \mu \le 3 \qquad H_A: \mu > 3 \end{align}$

the p-value is given by

$P(Z > 2.37)$

which we calculate with

1 - cdf(Z, 2.37)
#> [1] 0.008894043

For the test

$H_0: \mu \ge 3 \qquad H_A: \mu < 3$

the p-value is given by

$P(Z < 2.37)$

which we calculate with

cdf(Z, 2.37)
#> [1] 0.991106

Rejection regions

Preface: I am strongly opposed to make a dichotomous “reject/fail to reject” decision for hypothesis tests. If you do a hypothesis test, you should report the p-value, period. Picking an arbitrary $\alpha$ level rejection threshold and treating it as a gold standard is ridiculous, as evidenced by 60 years of statistical literature laden with warnings about hypothesis testing. That said, sometimes it can be useful to think about when you reject a hypothesis test.

We can think about three different rejection regions for a Z-test:

The rejection region in terms of the p-value
The rejection region in terms of the test statistic
The rejection region in terms of the sample mean

For a given $\alpha$ level threshold, all of these rejection regions are equivalent. We’ll start by thinking about the rejection of a two-sided test. That is

$\begin{align} H_0 : \mu = \mu_0 \qquad H_A : \mu \neq \mu_0 \end{align}$

We then calculate a test statistic $Z_\text{obs}$ , and a p-value $P(|Z| > |Z_\text{obs}|)$ and reject when $P(|Z| > |Z_\text{obs}|) < \alpha$ . This defines our first rejection region. Using our observation from before, this is exactly equivalent to rejecting when

$\begin{align} P(|Z| > |Z_\text{obs}|) < \alpha & \Longleftrightarrow 2 \cdot P(Z < -|Z_\text{obs}|) < \alpha \\ & \Longleftrightarrow P(Z < -|Z_\text{obs}|) < \alpha / 2 \end{align}$

and this last statement is exactly the same as when $Z_\text{obs} < z_{\alpha / 2}$ or $z_{1 - \alpha / 2} < Z_\text{obs}$ . This is our second region region, in terms of the test statistic. Finally, recall that

$Z_\text{obs} = \frac{\bar x - \mu_0}{\sigma / \sqrt{n}}$

So we take the conditions and rearrange to in terms of $\bar x$

$\begin{align} \frac{\bar x - \mu_0}{\sigma / \sqrt{n}} > z_{1 - \alpha / 2} & \Longleftrightarrow \bar x > \mu_0 + z_{1 - \alpha / 2} \frac{\sigma}{\sqrt n} \end{align}$

and

$\begin{align} \frac{\bar x - \mu_0}{\sigma / \sqrt{n}} < z_{\alpha / 2} & \Longleftrightarrow \bar x < \mu_0 + z_{\alpha / 2} \frac{\sigma}{\sqrt n} \end{align}$

You can also think about this in terms of $\mu_0$ . We will reject the test when $\mu_0$ is not in

$\begin{align} \left( \bar x + z_{\alpha / 2} \frac{\sigma}{\sqrt n}, \bar x + z_{1 - \alpha / 2} \frac{\sigma}{\sqrt n} \right) \end{align}$

which you may recognize as the confidence interval for $\mu$ ! So the confidence interval contains all the values of $\mu_0$ that we cannot reject at the $\alpha$ level. You can perform a similar calculation for a one sided test, resulting in a one-sided confidence bound, where one end of the interval is either $\infty$ or $-\infty$ .

Power and sample size calculations

Formulas for power

We want to make sure that we actually reject our null hypothesis in the case that it is false. That is, we would like to make sure that our test has high power. Mathematically, this means that $P(\text{reject } H_0 | H_0 \text{ is false})$ . The problem here is that $H_0$ can be wrong in many different ways: it could be that the true $\mu$ is $2$ , it could be $7$ , it could be $4.26$ . So to calculate power as formulated above is not really possible. However, we can calculate power for specific versions of “ $H_0$ is false”.

Let’s consider the case that $H_0$ is false, and in particular the true value of $\mu$ is $\mu_A$ . In this case, the power of our test is $P(\text{reject } H_0 | \mu = \mu_A)$ . Recall that we reject $H_0$ when $\bar{x} > \mu_0 + z_{1 - \alpha / 2} \frac{\sigma}{\sqrt n}$ or $\bar{x} < \mu_0 + z_{\alpha / 2} \frac{\sigma}{\sqrt n}$ , so the power of our test when $\mu = \mu_A$ is

$P(\text{reject } H_0 \left | \mu = \mu_A \right .) = P\left( \left . \bar x > \mu_0 + z_{1 - \alpha / 2} \frac{\sigma}{\sqrt n} \right | \mu = \mu_A \right) + P\left( \left . \bar x < \mu_0 + z_{\alpha / 2} \frac{\sigma}{\sqrt n} \right | \mu = \mu_A \right).$

Remember that $\bar X \sim \mathrm{Normal} \left(\mu, \frac{\sigma^2}{n} \right)$ . This means that, given $\mu = \mu_A$ , $\bar{x} \sim \mathrm{Normal} \left(\mu, \frac{\sigma^2}{n} \right)$ , which let’s us calculate the probabilities we need to find the power:

$\begin{align} P\left( \left . \bar{x} > \mu_0 + z_{1 - \alpha / 2} \frac{\sigma}{\sqrt n} \right | \mu = \mu_A \right) &= P\left( \frac{\bar{x} - \mu_A}{\sigma/\sqrt{n}} > \frac{\mu_0 + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} - \mu_A}{\sigma/\sqrt{n}} \right) \\ &= P\left( Z > \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{1-\alpha/2} \right), \end{align}$

and similarly

$P\left( \left . \bar{x} < \mu_0 + z_{\alpha / 2} \frac{\sigma}{\sqrt n} \right | \mu = \mu_A\right) = P\left( Z < \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{\alpha/2} \right).$

So, the power of our test, if the true population mean is $\mu_A$ , is

$\begin{align} \text{Power} &= P\left( Z > \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{1-\alpha/2} \right) + P\left( Z < \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{\alpha/2} \right) \\ &= \left[1 - P\left( Z < \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{1-\alpha/2} \right)\right] + P\left( Z < \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{\alpha/2} \right) \end{align}$

Let’s calculate this if $\mu_A = 5$ .

power_lower <- (3 - 5) / (2 / sqrt(10)) + quantile(Z, 0.025)
power_upper <- (3 - 5) / (2 / sqrt(10)) + quantile(Z, 1 - 0.025)

cdf(Z, power_lower) + (1 - cdf(Z, power_upper))
#> [1] 0.8853791

This means that the probability that we reject the null hypothesis ( $H_0: \mu = 3$ ) if the true mean is $5$ is about 0.89.

Formulas for sample size calculations

Often times researchers like to go in the other direction: aim for a specific level of power, and calculate how many observations are needed to reach that level. To achieve a power of $1 - \beta$ for a one sample Z-test with $H_0 : \mu = \mu_0$ , you need

$$ n \approx \left( { \sigma \cdot (z_{\alpha / 2} + z_\beta) \over \mu_0 - \mu_A } \right)^2 $$

samples. If $n$ is not an integer, round up. Often, the denominator is thought of as the detectable difference. So, the question becomes how many samples are required to have sufficient power to detect a difference of some particular size.

This equation is simply a rewrite of the equation presented above for power. Recall, the power for a two sided test is

$\text{Power} = P\left( Z > \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{1-\alpha/2} \right) + P\left( Z < \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{\alpha/2} \right).$

Usually, only one of these terms is contributing while the other is very close to zero. Let’s say the first term is the one clearly different from zero. To determine the sample size, we want to determine $n$ such that $P\left( Z > \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{1-\alpha/2} \right) = 1-\beta$ . Or, similarly, $P\left( Z < \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{1-\alpha/2} \right) = \beta$ . I.e. we need $\frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{1-\alpha/2} = z_{\beta}$ .

$\begin{align} z_{\beta} = \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} + z_{1-\alpha/2} & \Longleftrightarrow z_{\beta} - z_{1-\alpha/2} = \frac{\mu_0 - \mu_A}{\sigma/\sqrt{n}} \\ & \Longleftrightarrow \sigma (z_{\beta} - z_{1-\alpha/2}) = (\mu_0-\mu_A)\sqrt{n} \\ & \Longleftrightarrow \frac{\sigma (z_{\beta} - z_{1-\alpha/2})}{\mu_0-\mu_A} = \sqrt{n} \\ & \Longleftrightarrow \left(\frac{\sigma (z_{\beta} - z_{1-\alpha/2})}{\mu_0-\mu_A}\right)^2 = n \end{align}$

Since $z_{1-\alpha/2} = -z_{\alpha/2}$ , we have the equation above:

$\left(\frac{\sigma (z_{\beta} + z_{\alpha/2})}{\mu_0-\mu_A}\right)^2 = n.$

As an example, say the student prior to the experiment had determined that they wanted to test if the number of memes their professors know and love is 2. They want to make sure their sample size is large enough so that they are likely to reject the null hypothesis if the true number is 3. They determine that they want a probability of 0.9 of rejecting the null if the true number is 3. So, a sample size calculation looks like this:

$$ n \approx \left( { 2 \cdot (1.96 + 1.28) \over 2-3 } \right)^2 = 41.99 $$

So to make sure that they reject the null hypothesis with a probability of 0.9 if the true value is 3, they would have to ask 53 professors.

Below is this same calculation done in R. Remember, $\beta = 1-\text{Power}$ . Note the small discrepancy. This is due to rounding error.

(2 * (quantile(Z, 0.05 / 2) + quantile(Z, 1 - 0.9)) / (3 - 2))^2
#> [1] 42.02969