One sample sign tests • distributions3

Problem setup

Sometimes you want to do a Z-test or a T-test, but for some reason these tests are not appropriate. Your data may be skewed, or from a distribution with outliers, or non-normal in some other important way. In these circumstances a sign test is appropriate.

For example, suppose you wander around Times Square and ask strangers for their salaries. Incomes are typically very skewed, and you might get a sample like:

$8478, 21564, 36562, 176602, 9395, 18320, 50000, 2, 40298, 39, 10780, 2268583, 3404930$

If we look at a QQ plot, we see there are massive outliers:

incomes <- c(8478, 21564, 36562, 176602, 9395, 18320, 50000, 2, 40298, 39, 10780, 2268583, 3404930)

qqnorm(incomes)
qqline(incomes)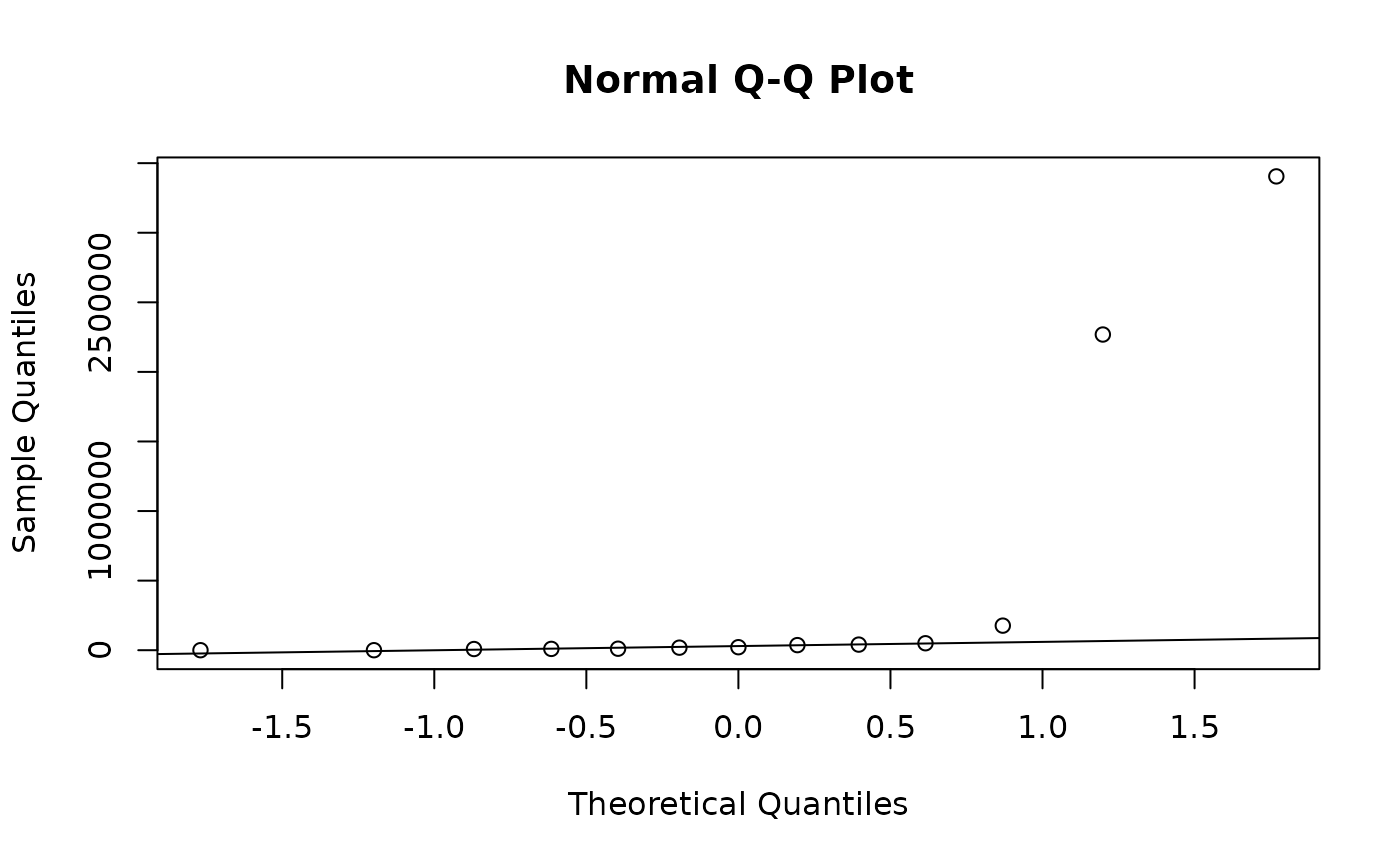

Luckily, the sign test only requires independent samples for valid inference (as a consequence, it has been low power).

Null hypothesis and test statistic

The sign test allows us to test whether the median of a distribution equals some hypothesized value. Let’s test whether our data is consistent with median of 50,000, which is close-ish to the median income in the U.S. if memory serves. That is

$H_0: m = 50,000 \qquad H_A: \mu \neq 50,000$

where $m$ stands for the population median. The test statistic is then

$B = \sum_{i=1}^n 1_{(50, 000, \infty)} (x_i) \sim \mathrm{Binomial}(N, 0.5)$

Here $B$ is the number of data points observed that are strictly greater than the median, and $N$ is sample size after exact ties with the median have been removed. Forgetting to remove exact ties is a very frequent mistake when students do this test in classes I TA.

If we sort the data we can see that $B = 3$ and $N = 12$ in our case:

sort(incomes)
#>  [1]       2      39    8478    9395   10780   18320   21564   36562   40298
#> [10]   50000  176602 2268583 3404930

We can verify this with R as well:

b <- sum(incomes > 50000)
b
#> [1] 3

n <- sum(incomes != 50000)
n
#> [1] 12

Calculating p-values

To calculate a two-sided p-value, we need to find

$\begin{align} 2 \cdot \min(P(B \ge 3), P(B \le 3)) = 2 \cdot \min(1 - P(B \le 2), P(B \le 3)) \end{align}$

To do this we need to c.d.f. of a binomial random variable:

library(distributions3)

X <- Binomial(n, 0.5)
2 * min(cdf(X, b), 1 - cdf(X, b - 1))
#> [1] 0.1459961

In practice computing the c.d.f. of binomial random variables is rather tedious and there aren’t great shortcuts for small samples. If you got a question like this on an exam, you’d want to use the binomial p.m.f. repeatedly, like this:

$\begin{align} P(B \le 3) &= P(B = 0) + P(B = 1) + P(B = 2) + P(B = 3) \\ &= \binom{12}{0} 0.5^0 0.5^12 + \binom{12}{1} 0.5^1 0.5^11 + \binom{12}{2} 0.5^2 0.5^10 + \binom{12}{3} 0.5^3 0.5^9 \end{align}$

Finally, sometimes we are interest in one sided sign tests. For the test

$\begin{align} H_0: m \le 3 \qquad H_A: m > 3 \end{align}$

the p-value is given by

$P(B > 3) = 1 - P(B \le 2)$

which we calculate with

1 - cdf(X, b - 1)
#> [1] 0.9807129

For the test

$H_0: m \ge 3 \qquad H_A: m < 3$

the p-value is given by

$P(B < 3)$

which we calculate with

cdf(X, b)
#> [1] 0.07299805

Using the binom.test() function

To verify results we can use the binom.test() from base R. The x argument gets the value of $B$ , n the value of $N$ , and p = 0.5 for a test of the median.

That is, for $H_0 : m = 3$ we would use

binom.test(3, n = 12, p = 0.5)
#> 
#>  Exact binomial test
#> 
#> data:  3 and 12
#> number of successes = 3, number of trials = 12, p-value = 0.146
#> alternative hypothesis: true probability of success is not equal to 0.5
#> 95 percent confidence interval:
#>  0.05486064 0.57185846
#> sample estimates:
#> probability of success 
#>                   0.25

For $H_0 : m \le 3$

binom.test(3, n = 12, p = 0.5, alternative = "greater")
#> 
#>  Exact binomial test
#> 
#> data:  3 and 12
#> number of successes = 3, number of trials = 12, p-value = 0.9807
#> alternative hypothesis: true probability of success is greater than 0.5
#> 95 percent confidence interval:
#>  0.07187026 1.00000000
#> sample estimates:
#> probability of success 
#>                   0.25

For $H_0 : m \ge 3$

binom.test(3, n = 12, p = 0.5, alternative = "less")
#> 
#>  Exact binomial test
#> 
#> data:  3 and 12
#> number of successes = 3, number of trials = 12, p-value = 0.073
#> alternative hypothesis: true probability of success is less than 0.5
#> 95 percent confidence interval:
#>  0.0000000 0.5273266
#> sample estimates:
#> probability of success 
#>                   0.25

All of these results agree with our manual computations, which is reassuring.