Draw a random sample from a hurdle Poisson distribution

Usage

# S3 method for class 'HurdlePoisson'
random(x, n = 1L, drop = TRUE, ...)

Arguments

x: A HurdlePoisson object created by a call to HurdlePoisson().
n: The number of samples to draw. Defaults to 1L.
drop: logical. Should the result be simplified to a vector if possible?
...: Unused. Unevaluated arguments will generate a warning to catch mispellings or other possible errors.

Value

In case of a single distribution object or n = 1, either a numeric vector of length n (if drop = TRUE, default) or a matrix with n columns (if drop = FALSE).

Examples

## set up a hurdle Poisson distribution
X <- HurdlePoisson(lambda = 2.5, pi = 0.75)
X
#> [1] "HurdlePoisson(lambda = 2.5, pi = 0.75)"

## standard functions
pdf(X, 0:8)
#> [1] 0.250000000 0.167672793 0.209590992 0.174659160 0.109161975 0.054580987
#> [7] 0.022742078 0.008122171 0.002538178
cdf(X, 0:8)
#> [1] 0.2500000 0.4176728 0.6272638 0.8019229 0.9110849 0.9656659 0.9884080
#> [8] 0.9965302 0.9990683
quantile(X, seq(0, 1, by = 0.25))
#> [1]   0   0   2   3 Inf

## cdf() and quantile() are inverses for each other
quantile(X, cdf(X, 3))
#> [1] 3

## density visualization
plot(0:8, pdf(X, 0:8), type = "h", lwd = 2)


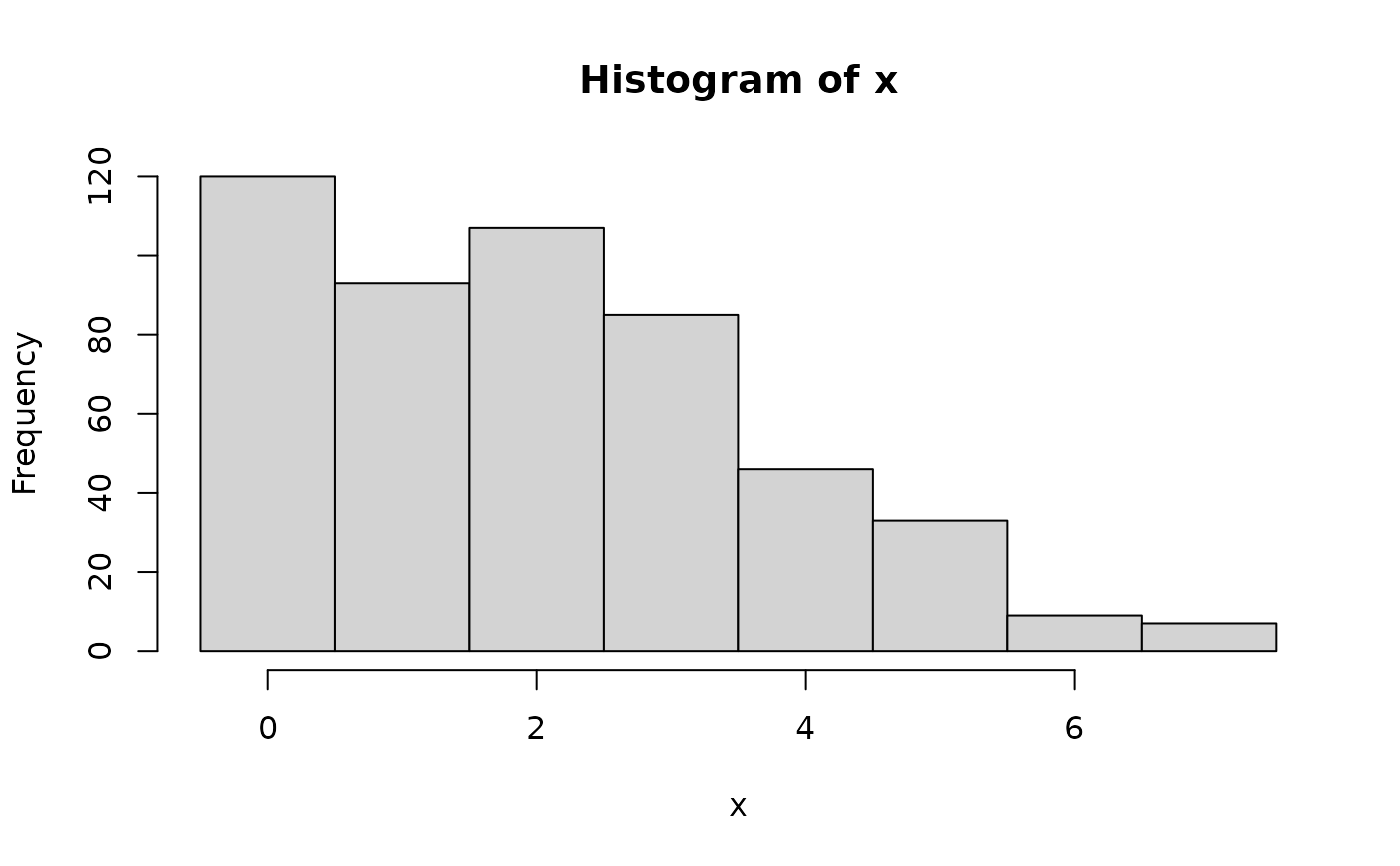
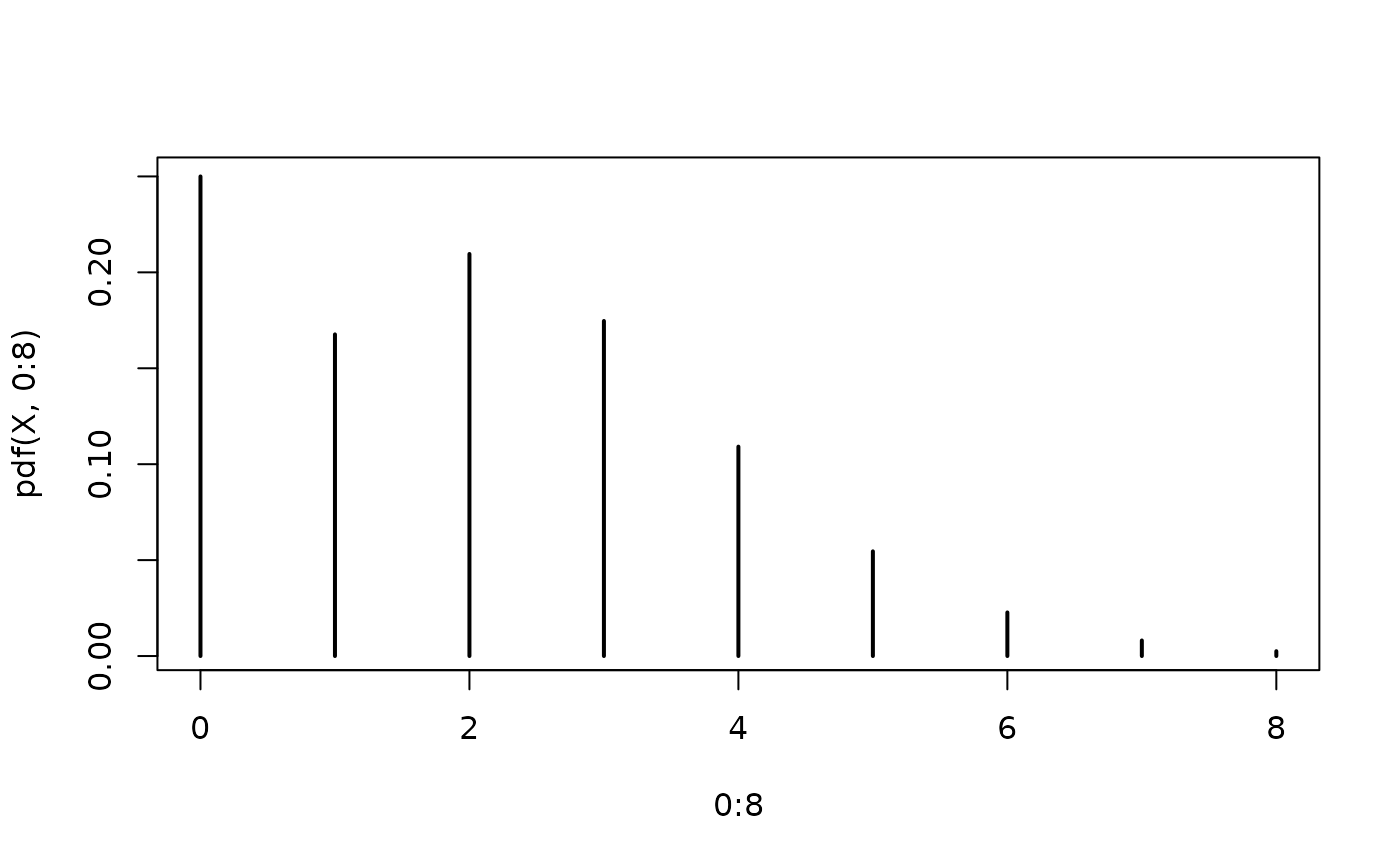## corresponding sample with histogram of empirical frequencies
set.seed(0)
x <- random(X, 500)
hist(x, breaks = -1:max(x) + 0.5)