Skip to contents

The hurdle Poisson distribution

Source: R/HurdlePoisson.R
hpois.Rd

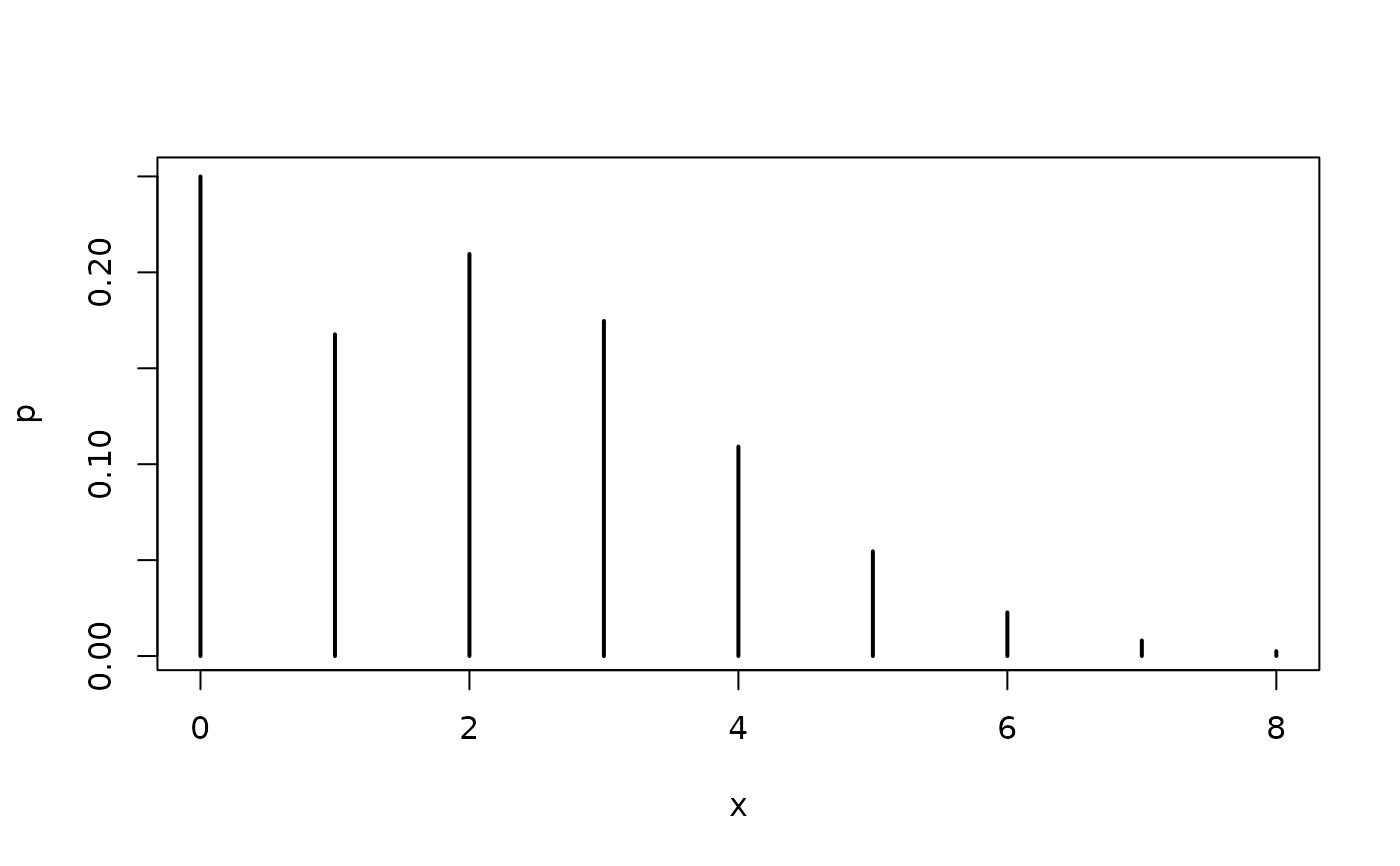
Density, distribution function, quantile function, and random generation for the zero-hurdle Poisson distribution with parameters lambda and pi.

Usage

dhpois(x, lambda, pi, log = FALSE)

phpois(q, lambda, pi, lower.tail = TRUE, log.p = FALSE)

qhpois(p, lambda, pi, lower.tail = TRUE, log.p = FALSE)

rhpois(n, lambda, pi)

Arguments

x

vector of (non-negative integer) quantiles.

lambda

vector of (non-negative) Poisson parameters.

pi

vector of zero-hurdle probabilities in the unit interval.

log, log.p

logical indicating whether probabilities p are given as log(p).

q

vector of quantiles.

lower.tail

logical indicating whether probabilities are \(P[X \le x]\) (lower tail) or \(P[X > x]\) (upper tail).

p

vector of probabilities.

n

number of random values to return.

Details

All functions follow the usual conventions of d/p/q/r functions in base R. In particular, all four hpois functions for the hurdle Poisson distribution call the corresponding pois functions for the Poisson distribution from base R internally.

Note, however, that the precision of qhpois for very large probabilities (close to 1) is limited because the probabilities are internally handled in levels and not in logs (even if log.p = TRUE).

See also

HurdlePoisson, dpois

Examples

## theoretical probabilities for a hurdle Poisson distribution
x <- 0:8
p <- dhpois(x, lambda = 2.5, pi = 0.75)
plot(x, p, type = "h", lwd = 2)


## corresponding empirical frequencies from a simulated sample
set.seed(0)
y <- rhpois(500, lambda = 2.5, pi = 0.75)
hist(y, breaks = -1:max(y) + 0.5)